Class-IX Unit-7 Triangles
Download Solution (Triangles)
What is Congruence
- In geometry, two figures or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other.
- A combination of rigid motions, namely a translation, a rotation, and a reflection is also permitted in Congruence. Translation means sliding,Rotation means turning and Reflection means Flipping. If two figures can be overlapped using translation,rotation or reflection then they are congurence
- It has come from Latin word congruere "agree, correspond with"
What is the difference between Congurence and Similarity?
Two Figures are similar if the objects differ in size but not in shape while in congurence size and shape remains sameWhy do we need to Learn it?
- We need to learn congurence in order to identify and describe many congurent object in real life. It may be some sculpture, some old monuments,
- In Pyramid, all the three triangular surface are congurent.AROUND 2600 B.C., construction of the Great Pyramid of Khufu began. It took the ancient Egyptians about 30 years to transform 6.5 million tons of stone into a pyramid with a square base and four congruent triangular faces
- We need several identical shirts button ,various factory part and many numerous objects. All these need the concept of Congurence
- Symbol used is ≅
- Two angles are congruent if they are equal
- Two circle are congruent if they have equal radii
- Two squares are congruent if the sides are equal
- Two line segments are congruent if they have equal length
- Two triangles are congruent if three sides and three angles of one triangle is congruent to the corresponding sides and angles of the other
- Corresponding sides are equal AB=DE , BC=EF ,AC=DF
- Corresponding angles are equal
- We write this as
ABC ≅ DEF - The above six equalities are between the corresponding parts of the two congruent triangles. In short form this is called C.P.C.T
- We should keep the letters in correct order on both sides
Congruence
Two Geometric figure are said to be congruence if they are exactly same size and shapeTriangle Congruence
Properties of Congurent triangles
1) Reflexive Property of Congurent Triangle: Every Triangle is congurent to itself
ABC ≅ ABC
2) Commutative or symmetric property of Congurent Triangle:
if ABC ≅ DEF then DEF ≅ ABC
3) Transitive Property Of congurent Triangle
if ABC ≅ DEF and DEF ≅ LKM then ABC ≅ LKM
Since Congurence relation satisfy Reflexive ,symmetric and Transitive ,it is an equivalence relation
Different Criterion for Congruence of the triangles
SAS Congurence (AXIOM)
ASA Congurence (Theorem)
SSS Congurence (Theorem)
RHS Congurence (Theorem)
How to Prove the congurence of Two Triangle
1) We have already studied that two triangles are congurent when all the sides and all the angles are equal. But we dont need prove all these while solving the Problem2) We just need to prove the congurence using the different criterio like SSS,ASA,SAS,RHS,AAS
3) Dont use AAA
4) Use the theorem learn in previous Geometry chapter like vertically opposite angles,alternate interior angles,corresonding angles
5)Write down the corresponding angles and corresponding sides carefully
6) We need to be careful with the labelling when our Triangles are in different positions
Inequality of Triangle
1) In a triangle angle opposite to longer side is larger- 2) In a triangle side opposite to larger angle is larger
3) The sum of any two sides of the triangle is greater than the third side
In triangle ABC
AB +BC > AC
4) Difference of any two sides of triangle is less than the third side
AC-AB < BC where AC > AB
Important defination for Triangles
Median
A line Segment joining the corner of the triangle to the mid point of the opposite side of the triangle. All the median of the triangle passes through the same pointCentroid
Point of intersection of the three median of the triangle is called the centroid of the triangle. The centroid divides each of the median in the ration of 2:1Altitude
A line Segment from the corner of the triangle and perpendicular to the opposite side of the triangle. All the altitude of the triangle passes through the same pointOrtho center
Point of intersection of the three altitude of the triangle is called the orthocenter of the triangle.Incenter
All the angle bisector of the triangle passes through same point .It is called incenter.Circumcenter
The perpendicular bisector of the sides of the triangles passes through same point. It is called circumcenter
Solved Example
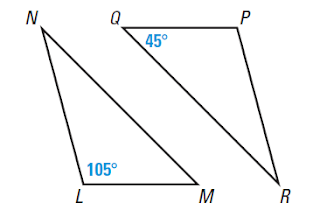
Write down the corresponding congurent sides?
Solution:
By Congurence, All the corresponding angles and corresponding sides are equal
LMN ≅ PQR
Steps to find the All the corresponding angles and corresponding sides
1) For angles, The First alphabet on right hand side corresponds to First alphabet on Left hand side,Similary second and third alphabet
So ∠ L=∠ P
∠M=∠ Q
∠ N=∠ R
Now ∠ L=1050
∠ Q=45, So ∠ M=45 0
∠P=1050
Now ∠ R can be found from the theorem
"Sum of the all the angles in a traingle is 1800"
So ∠ R=180-105-45=300
∠ N=30 0
2) For sides,The first two alphabet on right hand side corresponds to First two alphabet on Left hand side,Similary 2,3 and 3,1
LM=PQ
MN=QR
LN=PR
Solution:
By Congurence, All the corresponding angles and corresponding sides are equal
LMN ≅ PQR
Steps to find the All the corresponding angles and corresponding sides
1) For angles, The First alphabet on right hand side corresponds to First alphabet on Left hand side,Similary second and third alphabet
So ∠ L=∠ P
∠M=∠ Q
∠ N=∠ R
Now ∠ L=1050
∠ Q=45, So ∠ M=45 0
∠P=1050
Now ∠ R can be found from the theorem
"Sum of the all the angles in a traingle is 1800"
So ∠ R=180-105-45=300
∠ N=30 0
2) For sides,The first two alphabet on right hand side corresponds to First two alphabet on Left hand side,Similary 2,3 and 3,1
LM=PQ
MN=QR
LN=PR



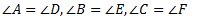







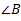
No comments