Class-IX Unit-11 Constructions
Introduction
Sometimes we need to create precise & accurate figures. Construction helps in creating these precise & accurate figures. Construction is used in designing Automobile, spaceships, building, roads etc.
We will need Protractor, Compass & Scale in this chapter.
Construction 1: To construct the bisector of a given angle ABC
Steps of Construction:
- Taking B as centre and any radius, draw an arc to intersect the rays BA and BC, say at E and D respectively
- Next, taking D and E as centers and with the radius more than 1/2 DE, draw arcs to intersect each other, say at F.
- Draw the ray BF . This ray BF is the required bisector of the angle ABC.
- Construction 2: To construct the perpendicular bisector of a given line segment.Steps of Construction:
- Taking A and B as centers and radius more than ½ AB, draw arcs on both sides of the line segment AB (to intersect each other). 2. Let these arcs intersect each other at P and Q.
- Join PQ. Let PQ intersect AB at the point M.
- Then line PMQ is the required perpendicular bisector of AB.
- Construction 3: To construct an angle of 600 at the initial point of a given ray.Steps of Construction:
- Taking A as centre and some radius, draw an arc of a circle, which intersects AB, say at a point D.
- Taking D as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point E.
- Draw the ray AC passing through E. Then ∠ CAB is the required angle of 60°.
- Some Constructions of TrianglesConstruction 4: To construct a triangle, given its base, a base angle and sum of other two sides.Steps of Construction:
- Draw the base BC and at the point B make an angle, say XBC equal to the given angle.
- Cut a line segment BD equal to AB + AC from the ray BX.
- Join DC and make an angle DCY equal to ∠BDC.
- Let CY intersect BX at A. Then, ABC is the required triangle
- Construction 5: To construct a triangle given its base, a base angle and the difference of the other two sidesGiven the base BC, a base angle, say ∠B and the difference of other two sides AB – AC or AC – AB, you have to construct the triangle ABC. Clearly there are following two cases:Case (i) : Let AB > AC that is AB – AC is given.Steps of Construction:
- Draw the base BC and at point B make an angle say XBC equal to the given angle.
- Cut the line segment BD equal to AB – AC from ray BX.
- Join DC and draw the perpendicular bisector, say PQ of DC.
- Let it intersect BX at a point A. Join AC. Then ABC is the required triangle
- Case (ii) : Let AB < AC that is AC – AB is given.Steps of Construction:
- Draw the base BC and at point B make an angle say XBC equal to the given angle.
- Cut the line segment BD equal to AC – AB from line BX extended on opposite side of line segment BC.
- Join DC and draw the perpendicular bisector, say PQ of DC.
- Let PQ intersect BX at A. Join AC. Then, ABC is the required triangle.
- Construction 6: To construct a triangle, given its perimeter and its two base angles.Steps of Construction:
- Draw a line segment, say XY equal to BC + CA + AB.
- Make angles LXY equal to ∠B and MYX equal to ∠C.
- Bisect ∠LXY and ∠ MYX. Let these bisectors intersect at a point A .
- Draw perpendicular bisectors PQ of AX and RS of AY.
- Let PQ intersect XY at B and RS intersect XY at C. Join AB and AC . Then ABC is the required triangle.












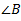
No comments