Class-IX Unit-10 Circle

Download Solution (Circle)

Introduction

The collection of all the points in a plane, which are at a fixed distance from a fixed point in the plane, is called a circle.

Lot of things around us are circular in shape, such as car tires, shirt buttons, Bangles, Coin, Bottle cap, Football, Earth, Sun. The path traced by tip of second or minute hand of clock is circular.

Steps to draw a circle:

Take c compass & fix a pencil in it
Put its pointed led on a point on a sheet of paper
Open the other leg to some distance, r.
Keeping the point leg on the same point rotate the other leg through one revolution
Closed figure traced by the pencil is called circle
One fixed point is called center of circle. Point A in figure below is Center
Fixed distance is called radius. Distance AB in figure below is radius.

Circle dividing the plane: Circle divides the plane on which it lies into three parts. They are:

inside the circle, which is also called the interior of the circle;
the circle and
Outside the circle, this is also called the exterior of the circle.

The circle and its interior make up the circular region.

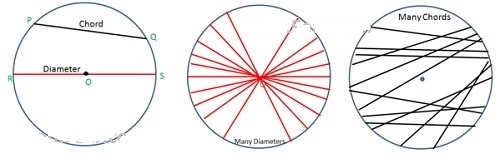
hord & Diameter

Take any two points P & Q on Circle & join these two points to get Chord PQ. There can be infinite number of chords in a given circle of various lengths.

Longest chord is called diameter & it passes through center & has length 2r. RS is the diameter in the figure shown. You can have infinite number of diameters for a given circle. All these diameters will be same length 2r.

Minor & Major Arc

Piece of circle between two points is called Arc.

In the figure shown, notice that there are 2 pieces formed using points P & Q. One piece is smaller in Size & is in RED color, while the other piece is bigger in Size & is in BLUE color. Longer Arc is called Major arc & shorter arc is called Minor Arc.

When P and Q are ends of a diameter, then both arcs are equal and each is called a semicircle.

Minor & Major Segment

The region between a chord and either of its arcs is called a segment of the circular region or simply a segment of the circle. There are two types of segments, major segment and the minor segment. Minor arc corresponds to the minor segment and the major arc corresponds to the major segment.

In the figure given, region in cream color is Major segment & Region in grey color is minor segment.

When two arc are equal, that is each is a semicircle then both the segments are called Semicircular region.

Perpendicular from center to a chord

Theorem 3: The perpendicular from the centre of a circle to a chord bisects the chord.

In the given figure, If line OC is drawn perpendicular from center O to Chord AB. It is observed that C divides line AB into two equal part, that is AC=CB.

Refer ExamFear video lessons for Proof of this theorem

onverse Theorem 4: The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.

In the given figure, C is the midpoint of chord AB. Line OC is drawn from center O to C,it is observed that OC is perpendicular to AB.

Refer ExamFear video lessons for Proof of this theorem

Circle through 3 points

Let’s draw circles through 1, 2 & 3 points. We can see in the figure that infinite number of circles can be drawn through 1 or 2 points.

Also notice that only one Circle can be drawn using 3 non-collinear points.

Also a circle can’t be drawn using 3 collinear points.

Theorem 5: There is one and only one circle passing through three given non-collinear points.

Refer ExamFear video lessons for Proof of this theorem

Equal chords & their distance from center

In the given figure, we have to find distance of point P from line AB. We can draw multiple lines from point P to line AB, such as PC, PD, PE, PF, PG ,PA, PB. All these lines are of different length. So, we consider. the length of the perpendicular PE from a point P to a line AB as the distance of the line from the point.

Also notice that the length of the perpendicular PE from a point P to a line AB is the least distance. That is PE is smallest of PA, PB, PC, PD, PE, PF, PG etc.

If point P lines on Line AB, then the perpendicular distance is 0.

Length of chord & distance from center: A circle can have infinitely many chords. In the figure given we observe that longer chord is nearer to the centre than the smaller chord. Diameter is the longest chord from the centre, since the centre lies on it, the distance is zero. AB is the longest chord in the figure shown & IJ is the shortest chord. Also observe that distance of AB is shortest from center & that of IJ is largest.

Theorem 6: Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centers).

In the figure, if Chord AB= CD, then it is observed that perpendiculars OP = OQ

Converse Theorem 7: Chords equidistant from the centre of a circle are equal in length.

In the figure, if perpendiculars OP = OQ, then it is observed that chord AB= CD.

Angle Subtended by Arc of Circle

If two chords of a circle are equal, then their corresponding arcs are congruent and conversely, if two arcs are congruent, then their corresponding chords are equal. If Arc AB = Arc CD, then Chord AB = Chord CD.

Congruent arcs (or equal arcs) of a circle subtend equal angles at the centre. In the figure, Arc AB = Arc CD & thus, it is observed that ∠1 =∠2..

Theorem 8: The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.

In the figure shown that ∠2 =Twice of ∠1.

Theorem 9: Angles in the same segment of a circle are equal

In the figure, ∠1 = ∠3.

onverse Theorem 10: If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle (i.e. they are concyclic).

In the figure, if ∠1 = ∠3, then point A, B, C & D lies on a circle.

Cyclic Quadrilateral

A quadrilateral ABCD is called cyclic if all the four vertices of it lie on a circle