Class-IX Unit-6 Line and Angles
Download Solution (Line and Angles)
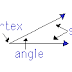
What is angle
An angle is a formed of two rays with a common endpoint. The Common end point is known as the vertex of the angle and the rays as the sides, sometimes as the legs and sometimes the arms of the angle
We denote the angle by symbol ∠
If A is the Vertex,then angle could be represented as ∠A
Types of Angle
As the angle size is increased,it is termed with different name.Degree and Radian
They both are unit of measurement of angles
Radian: A unit of measure for angles. One radian is the angle made at the center of a circle by an arc whose length is equal to the radius of the circle.Degree: If a rotation from the initial side to terminal side is (1/360) of a revolution, the angle is said to have a measure of one degree, written as 1°. A degree is divided into 60 minutes, and a minute is divided into 60 seconds . One sixtieth of a degree is called a minute, written as 1", and one sixtieth of a minute is called a second, written as 1'.
Thus, 1° = 60', 1' = 60"
Relation between Degree and Radian
2π radian = 360 ° π radian= 180 ° 1 radian= (180/π) °
| Degree | 30° | 45° | 60° | 90° | 120° | 180° | 360° |
| Radian | π/6 | π/4 | π/3 | π/2 | 2π/3 | π | 2π |
Congruence Angle
Two angles are said to be congruent if they are having same measure
∠A=300∠B=300
then
∠A=∠B
They are congurent
Adjacent Angles
Two angles are called adjacent angles if they share the same vertex,they have a common arm. The second arm of the one angle is one side and second arm of other angle is on the other side
Here the sum of angles =900
Supplementary Angles
Two angles , the sum of whose measures is 1800 is called Supplementary Angles.Each of these Supplementary Angles are called the suplement of each other
Linear Pair Axioms
If a ray stands on a line, then the sum of the adjacent angles so formed is 1800
And If the sum of the adjacent angles is 1800,then the non common arms of the angles form a line
Theorem Based on Linear Pair Axiom
The sum of all the angles around a point is 3600Vertically Opposite angles
If two lines intersect with each other, then vertically opposite angles are equal
Transversal across the parallel Lines
If the transversal intersect two parallel lines as shown in below figure
Important Take aways from the figure
1) We can see following angles as depicted in the figure above∠1,∠2,∠3,∠4 on the first parallel line
and ∠5,∠6,∠7,∠8 on the second parallel line
2) The angles 1,2,6,7 are called exterior angles while the angles 4,3,5,8 are called interior angles
3) Corresponding Angles:The angles on the same side of the Transversal are known as Corresponding angles
And Corresponding Angles axiom states that

4) Each pair of alternate interior angles are equal
5) Each pair of interior angles on the same side of the transversal is supplimentary
Converse of Transversal across the parallel Lines
If a transversal intersect two lines such that either
a) any one pair of corresponding angles are equalb) any one pair of alternate interior angles are equal
c) any one pair of interior angles on the same side of the transversal is supplimentary
Then the two lines are parallel
Parallel lines Note
Lines which are parallel to a given line are parallel with each other


















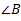
No comments